How To - Determinants of Matrices
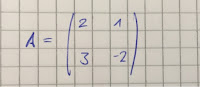
The determinant of a matrix is very useful and commonly asked for in exams. With it, you can determine if a matrix is invertible (thus find the inverse for sure, without wasting tons of precious time in an exam) and it's a sure way to get points even if you are pretty hopeless and just want to pass There are three basic cases for matrices, dimensions 2x2 , 3x3 and dimensions 3< . Results for the three exercises will be posted at the end. Tipp : a matrix can only be inverted if the determinant does not equal 0 ! In the case of matrix A (2x2) the main- minus minor-diagonal formula applies; with upper left times lower right, minus upper right times lower left. For example B (3x3) it becomes more complicated. We can apply the rule of Sarrus ( Wikipedia ). For that, we replicate the first two columns to the right side. Now we create the main and minor diagonals, as seen in the picture below: After this, we subtract the sum of the minors from the sum of the...