How To - Determinants of Matrices

The determinant of a matrix is very useful and commonly asked for in exams. With it, you can determine if a matrix is invertible (thus find the inverse for sure, without wasting tons of precious time in an exam) and it's a sure way to get points even if you are pretty hopeless and just want to pass

There are three basic cases for matrices, dimensions 2x2, 3x3 and dimensions 3<.
Results for the three exercises will be posted at the end.

Tipp: a matrix can only be inverted if the determinant does not equal 0 !

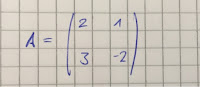
In the case of matrix A (2x2) the main- minus minor-diagonal formula applies; with upper left times lower right, minus upper right times lower left.

For example B (3x3) it becomes more complicated. We can apply the rule of Sarrus (Wikipedia). For that, we replicate the first two columns to the right side. Now we create the main and minor diagonals, as seen in the picture below:

After this, we subtract the sum of the minors from the sum of the main diagonals and receive the determinant :)

Example C is a lot more work, but usually asked for in exams as it is basically includes the rule of Sarrus.

Try to pick the column or row with the most zeros or ones, in this case we of course choose the third row.

Starting with 1. we cancel out the first column, and create a 3x3 matrix out of the remaining 9 numbers. 

Then we do the same with 2. this time for the second column and so on for 3. and 4.

We will be needing the determinants for each of these matrices and multiply them with the factor, which is the digit 1 to 4 of the third row.

The determinants which are multiplied with factor 0 can just be canceled out - now you see why we picked the row with the most zeros :D

Solutions: det(A) = -7; det(B) = -5; det(C) = 60