How To - Complex Numbers

We have reached the part about my studies which I don't enjoy so much.
Math. 
There is of course lots more to it than the few tutorials I can upload - especially since right now I am really busy studying for the exams to come, but here you go!

 A How-To about calculating with Complex Numbers (takes up to 10min to understand)

 The first part here focuses on complex numbers in their algebraic form, I will edit this tutorial however, to show you the polar-coordinate form, as soon as I have time :p

 When starting out with this topic, you will soon encounter the variable i .
Because i is defined as i^2 = -1 we can extend our Real Numbers so that the formula becomes solvable: x^2 +1 = 0


In the algebraic form complex numbers are written as z = x + iy


If you want to work with complex numbers, these 4 rules will help you solve the test question at the end :)

1. Addition





2. Subtraction


3. Multiplication





4. Division

In division it can become a bit chaotic, just keep your head calm and form the conjugate of the denominator, and add it like so to our equation:











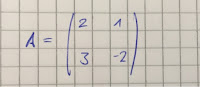
Exercise for the nerdy ones: 
z = i/(1-2i)^2 

Hope this was helpful to you guys :)


Solution to the exercise:
(4/25) - (3i/25)

Comments

Post a Comment

Popular posts from this blog

How To - Variance & Standard Deviation

Image
Hey Guys, today we do a quick intro on some basic terms and formulas that are used frequently in statistics - Mode or Modal Value, Middle Value, Median, Variance and the Standard Deviation We have a class of 8 Girls and 8 Boys , so a total of 16 kids . To get the Modal Value (m) and therefore represent the level of the whole class, we count how often each grade showed up - in our case 2 and 3 Next comes what probably everyone did at least once in school; calculate the class average or our Middle Value (a small X with a line over its top; sorry I can't write it out here .__. ) Using the Median is actually just being nit-picky, but good to know. In case your teacher breaks into your house in the middle of the night and wants to know... you will probably never use this one in your life For uneven : look for the middle number For even : look for the two middle numbers, sum them up and divide by 2 - that's your median The formula for Variance may look difficult at first,...
Read more

How To - CYK Algorithm

Image
In this quick post I try to explain the basics of the Cock-Younger-Kasami ( CYK ) Algorithm to you. This shouldn't take more than 15min for you to understand, since I am terrible at logic and math related studies - if I could do it so can you :D The CYK is a theoretical construct that can be used to find context free languages by feeding grammar and its production rules into a table and see wether a word from the language you wish to identify, matches up with these rules. To make this process run smooth, the production rules must be formatted in such way that it matches Chomsky Normal Form ( CNF ) standards; on the left hand side of a production rule stands a non-terminal symbol (a variable) on the right hand side of a production rule there can be maximal 2 non-terminals or 1 terminal symbol (a symbol that represents a constant value) but never non-terminals and terminals mixed For my course I worked through an example step by step, we started out with 3 production rules: A...
Read more

How To - Citric Acid Cycle

Image
The citric acid cycle is one of the central logistical hub in our metabolism. It provides oxidative breakdown for organic substances, energy by releasing CO2 and H2O from Acetyl-CoA and so on. There are 10 basic steps to the cycle and its goal is to catalyze the condensation of Oxalacetate to Citrate. I will list the  intermediates of this reaction and their respective enzymes , as well as their components : Citrate  + Aconitase -> cis-Aconitate   ( H20) cis-Aconitate + Aconitase ->  Isocitrate    ( H20) Isocitrate  + Isocitrate-dehydrogenase -> Oxalsuccinate    (NAD+, NADH) Oxalsuccinate  + Isocitrate-dehydrogenase -> Alpha-ketoglutaric-acid   (CO2) Alph a-ketoglutaric-acid  + alpha-ketoglutarate-dehydrogenase-complex -> Succinyl-CoA   (CoA, NAD+, CO2, NADH/H+) Succinyl-CoA  + Succinyl-CoA-Synthase -> Succinate  (GDP, ADP, GTP, ATP) Succinate...
Read more